最近在学习后端优化的前沿知识，发现其中有些部分之前理解的还不是很清楚，因此专门挑了个时间对后端优化进行了稍微系统性一些的学习。这篇blog就将梳理一下 Pose Graph Optimization 的研究脉络，以及一些传统的方法与技巧。后续也将在此基础上进一步分享前沿 PGO 的研究成果。
1. 背景知识
接触过SLAM系统的同学应该都对位姿图有所耳闻。SLAM问题主要可以分为滤波和图优化两类，滤波算法以扩展卡尔曼滤波（EKF）为例，它的输入是当前时刻状态、观测以及运动模型，输出则是下一时刻的状态，这其实是假设了马尔可夫性质，即下一时刻状态仅与当前状态相关，因此其计算量较小，能够在资源约束的条件下运行，但其需要存储地标对应的状态，因此在长时间大范围的场景下也有性能问题，一般有滑动窗口以及边缘化操作来应对这个问题。图优化的方法并不频繁地校正位姿，而是将历史信息记录下来，构成一个图（graph），在有闭环等校正情况时，再去统一校正历史信息。
在图优化中，构建的图我们称之为位姿图，因为图的每个节点（vertex）代表了一个机器人的位姿，位姿之间的关系则组成了边（edge），实际应用过程中，边信息一般由里程计的输出决定。因为里程计的定位会又累积误差，因此引入全局定位来减小误差。全局定位的信息在图中也表示为边，这类边一般能够提供较强的优化约束，因为它将原始的简单的图结构构成了一个环，为优化问题提供了一个强约束项。在一个具有环形结构的图构建完成后，位姿图优化就是要去调整机器人的位姿以尽量满足这些边构成的约束。
图优化的步骤大致就可以分为以下两步：1、（前端）位姿图构建；2、（后端）图优化
2. 优化问题构造
2015年，Luca Carlone 在机器人顶会 ICRA 上发表了一篇综述，针对位姿图优化的初始化问题进行了文献整理与分析。本文是在此基础上进行扩展而成的，如果有兴趣，大家可以去学习一下原文。
Carlone L, Tron R, Daniilidis K, et al. Initialization techniques for 3D SLAM: a survey on rotation estimation and its use in pose graph optimization[C]//2015 IEEE international conference on robotics and automation (ICRA). IEEE, 2015: 4597-4604.
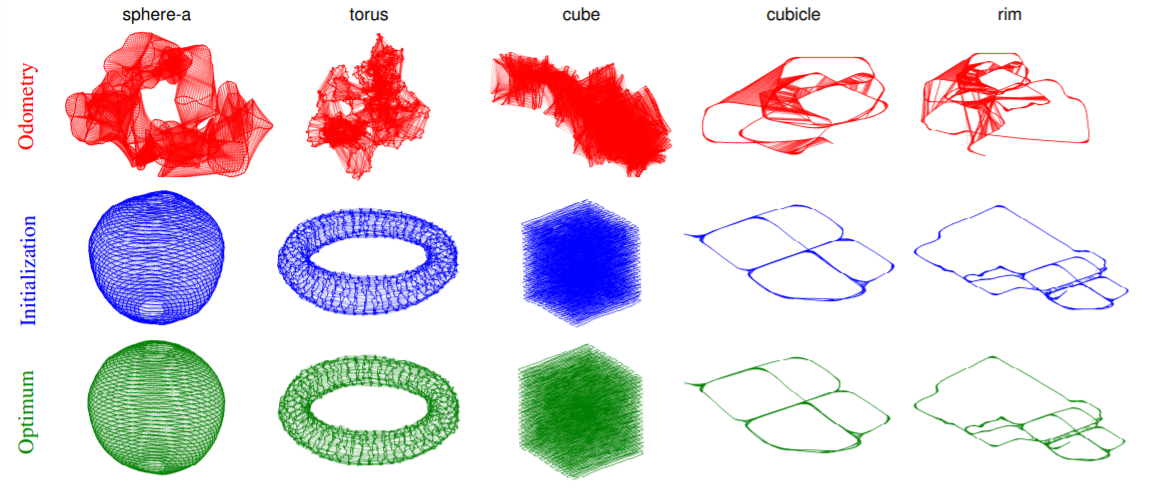
上面是一个位姿图的可视化，原始位姿图具有较大的噪声，通过旋转估计初始化后得到的位姿图则与真实的图非常接近。右边两列位姿图是真实环境中获取的，说明PGO可以真实的应用于现实系统。
位姿优化部分做的事情是从m个相对位姿测量中估计n个机器人的位姿。这里的位姿属于SE(3)，其中旋转部分是属于SO(3)的。这里不太清楚的话可以去看一下高翔博士的《视觉SLAM十四讲》。有了这些基本知识，以及对图模型的基本概念之后，我们就可以列出一个优化问题。
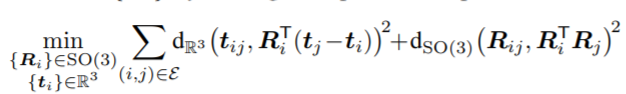
这里的d是distance的缩写，平移的距离就是欧氏距离，而旋转的距离则有很多种选择，在2.2部分会提到。这个优化问题是非凸的，因为该式需要满足旋转矩阵的SO(3)限制，因此无法直接应用高斯牛顿等方法。注意到方程可以由加号分为两个部分，加号后一项只与旋转相关。如果我们首先对旋转进行估计，并将估计量带入方程加号前面的一项（平移项），那对平移的估计就是一个线性的最小二乘问题，可以用高斯牛顿的方法求解。这样的一个思路其实就是将原有同时优化旋转平移的问题，分解到旋转估计问题上。下式就是旋转估计问题的数学表达。旋转估计初始化的思想就是首先求解这个估计问题，然后将估计出来的旋转当做初值去迭代求解之前的带平移的估计问题。这样的问题分解方式使得计算可以加速。
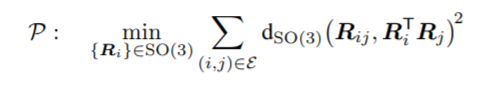
求解上式首先需要一点旋转相关的预备知识，这里推荐一篇发表在2013年 IJCV 上的一篇文章，介绍了旋转平均的相关理论。
Hartley R, Trumpf J, Dai Y, et al. Rotation averaging[J]. International journal of computer vision, 2013, 103(3): 267-305.
2.1 旋转表示 (熟悉的朋友可以跳过)
-
李群 SO(3)：正交的3x3矩阵R，且R的行列式为1。
-
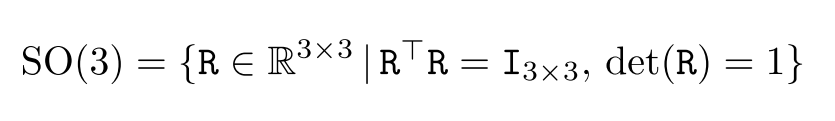
对应$SO(3)$李群，有李代数$so(3)$，它是反对称3x3矩阵的集合。连接李群和李代数的桥梁是指数映射（exponential map），取李代数中的元素 $\Omega \in so(3)$, 指数映射为$exp(\Omega)$，其结果就是李群中的对应元素，这个映射是满射的。一个李代数的反对称阵又可以由一三元素的向量表示。$v=(v_1,v_2,v_3)^T$。
-
李群中还有对应的李括号，不过在此处不常用。
-
-
轴角：每个$SO(3)$中的旋转可以表示为一组$\theta$对应一组单位向量$\hat{v}$，$v=\theta\hat{v}$，轴角的表示不是唯一的，$(2\pi-\theta)(-\hat{v})=\theta\hat{v}$。轴角和李群的对应关系是由$exp[\cdot]_\times$, 此处的 $[\cdot]_\times$在有些地方也用$[\cdot]^{\wedge}$表示，这个对应关系即给定一个$v=\theta\hat{v}$， $exp[v]_\times$的结果就是对应的旋转矩阵。这个映射连接了$\mathbb{R}^3$ 和 $ SO(3)$。在这里我们也将$exp[\cdot]_\times$称为指数映射，它的逆运算则称为对数映射$log(\cdot):SO(3)\rightarrow \mathbb{R}^3$。
-
通俗一点来说，用单位向量$\hat{v}$代表旋转轴，以及$\theta$代表绕该轴的旋转角度。则可以用三维向量$\hat{v}θ\in\mathbb{R}^3$以指数形式来描述旋转。如果将$\hat{v}$和$\theta$分开描述，即为轴角形式。
-
指数映射可以用罗德里格斯公式（Rodrigues’ formula）进行计算: $$ exp[\theta\hat{v}]=I+\sin\theta[\hat{v}]_\times+(1-cos\theta)([\hat{v}]_\times)^2 $$ 对数映射则可以通过下式进行计算： $$ log(R)=\arcsin(||y||_2)\frac{y}{||y||_2}, y\neq0 $$ 此处的$y=(y_1,y_2,y_3)$，可以从下式导出： $$ \frac{1}{2}(R-R^T)=\begin{pmatrix} 0 & -y_3 & y_2 \\ y_3 & 0 & -y_1 \\ -y_2 & y_1 & 0 \end{pmatrix} \quad $$
-
-
四元数：$\mathbb{R}^4$中的非零实数向量。单位四元数组成了一个李群，同时也是一个三维流形。
-
四元数的乘法运算，令$\boldsymbol{r_1}=(c_1,\boldsymbol{v_1})$, $\boldsymbol{r_2}=(c_2,\boldsymbol{v_2})$.
\[\boldsymbol{r_1}\cdot\boldsymbol{r_2}=(c_1c_2-\langle\boldsymbol{v_1},\boldsymbol{v_2}\rangle, c_1\boldsymbol{v_2}+c_2\boldsymbol{v_1}+\boldsymbol{v_1}\times\boldsymbol{v_2})\]此处的$\langle\cdot\rangle$是标准的向量内积，$\times$为标准的叉乘。
-
另一种更为常见的乘法将四元数$\boldsymbol{r}=(r_0,r_1,r_2,r_3)$表示为$\boldsymbol{r}=r_0+r_1\boldsymbol{i}+r_2\boldsymbol{j}+r_3\boldsymbol{k}$, 其中$r_0$为四元数的实数部分。$\boldsymbol{i},\boldsymbol{j},\boldsymbol{k}$则是对应的虚数部分。定义了以上基本元素后，四元数的乘法运算就可以利用乘法分配率计算：$(r_0+r_1\boldsymbol{i}+r_2\boldsymbol{j}+r_3\boldsymbol{k})(s_0+s_1\boldsymbol{i}+s_2\boldsymbol{j}+s_3\boldsymbol{k})$, 其中$\boldsymbol{i}\cdot\boldsymbol{i}=\boldsymbol{j}\cdot\boldsymbol{j}=\boldsymbol{k}\cdot\boldsymbol{k}=\boldsymbol{i}\cdot\boldsymbol{j}\cdot\boldsymbol{k}=-1$
- 四元数的重要性质：
- $||\boldsymbol{q_1}\cdot\boldsymbol{q_1}||=||\boldsymbol{q_1}||||\boldsymbol{q_2}||, ||\boldsymbol{q}||$ 为向量范数。
-
单位向量：$(1,0,0,0)$
- 逆：$\boldsymbol{r}=(c,\boldsymbol{v})\rightarrow\boldsymbol{r}^{-1}=(c,-\boldsymbol{v})/||\boldsymbol{r}||^2$
-
四元数表示旋转：旋转$R$可以表示为一个单位四元数$\boldsymbol{r}$，$\boldsymbol{\hat{v}}$是一个单位轴，$\theta$是单位轴上的旋转，则
$$\boldsymbol{r}=(cos(\theta/2),\boldsymbol{\hat{v}}sin(\theta/2))$$, 通过这个和轴角的变换，四元数就可以与旋转矩阵$SO(3)$进行关联。
-
-
球心投影
-
射影几何
2.2 SO(3)上的距离表示
-
双不变距离：$d:SO(3)\times SO(3) \rightarrow \mathbb{R}^+$, $d(SR_1,SR_2)=d(R_1,R_2)=d(R_1S,R_2S)$
-
角距离：$SO(3)$上的旋转可以表示为沿着给定轴旋转的角度$\theta$, 在计算角距离时规定该角度在$[0，\pi]$，于是有
$$d_\angle(R_a,R_b)=d_\angle(R_aR_b^T,I)=||log(R_aR_b^T)||_2$$
-
弦长距离：$d_{chord}(R_a,R_b)=||R_a-R_b||_F=||R_a^TR_a-I_3||_F$
-
四元数距离：$d_{quat}(R_a,R_b)=min(||q_a-q_b||,||q_a+q_b||)$，此处$min$是用于消除符号歧义的，因为$q_a$和$-q_a$表示的旋转是一样的。
2.3 3D旋转估计
2.3.1 单回环解法：
利用角距离求解特殊单回环问题。原问题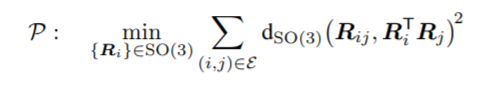： 转换为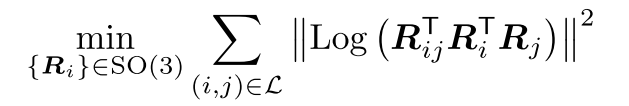
其中$L$是一个有序集$L={(1,2),(2,3),…,(n-1,n),(n,1)}$，这个问题的直觉解法是相对旋转在回环后为一个单位阵，但由于旋转测量具有噪声，使得相对旋转的累积量在回环后并不是单位阵。因此旋转估计器需要将多余的旋转分量最优地分配到各个边上，这也可以叫做 Rotation averaging。
在旋转估计时，本质上是对相对关系的优化，因此将上述带有节点旋转的绝对信息转为相对信息。定义：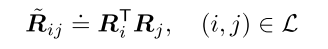
利用这个构造上述优化问题可以重写为：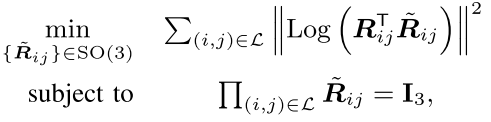
我们可以用非常直觉的方法解释这个构造：我们需要找到旋转$\tilde{R}{ij}$能够尽可能接近测量值${R}{ij}$同时又能够满足回环的要求。进一步改造这个方程，引入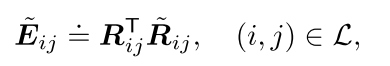
重写优化方程： 
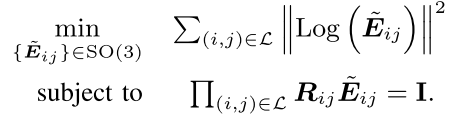这个优化问题也有一个直觉的解释：我们寻找一个小的校正$\tilde{E}_{ij}$使得回环的约束条件能够满足。进一步的，我们将这个重新排列旋转，那么上式中的约束可以写为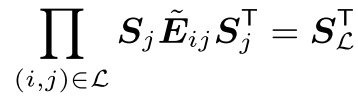
其中$S_j$表示j之前所有旋转的乘积,它的转置也就是逆是使得其最后回环为单位阵的要素，$S_L$表示所有旋转中我们需要补偿的“超过”部分。这里将连乘符号内部的符号定义为$\tilde{T}_{ij}$，带入优化方程中得到：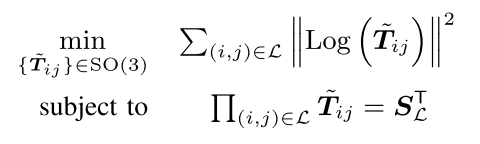
该公式表明我们需要找到一系列旋转$\tilde{T}_{ij}$，这些旋转的总和为一个已知的旋转”超过“部分，并使得这一系列旋转的角范数之和最小。这个优化方程的最优解为：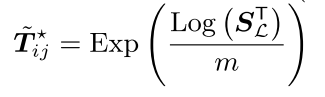
2.3.2 多回环
多回环多用迭代优化的方法求解，目前无法保证迭代的最优收敛性。可以参考文章
1、G. Dubbelman and B. Browning, “Closed-form online pose-chain slam,” in IEEE Intl. Conf. on Robotics and Automation (ICRA), 2013.
2、J. R. Peters, D. Borra, B. Paden, and F. Bullo, “Sensor network localization on the group of 3D displacements,” SIAM Journal on Control and Optimization, submitted, 2014.
3、V. Govindu, “Lie-algebraic averaging for globally consistent motion estimation,” in IEEE Conf. on Computer Vision and Pattern Recogni- tion (CVPR), 2004
